永磁步進電動機磁場的計算
郭 宏 王宗培 郭慶吉 劉桂芝(哈爾濱工業(yè)大學(xué))
l 引 言
為了保證步進電動機合理設(shè)計和可靠運行,需運用數(shù)值解法計算電機的磁場。電機電磁場的數(shù)值解法中,有限元法最常用。在有元法的整個計算過程中,非線性方程組的求解占有關(guān)鍵的地位。由于電機磁路中鐵磁材料部分的磁飽和特性,使得所建立的非線性方程組具有較復(fù)雜的結(jié)構(gòu)形式,這就常常引起非線性方程組求解過程的不收斂性。本文通過對一臺二相永磁步進電動機空載磁場的實際解算,具體分析非線性方程組求解過程中出現(xiàn)的不收斂性,并采用可變步長的牛頓一拉斐森法解決牛頓一拉斐森法(定步長)大范圍不收斂,使得迭代初值的選取具有較大的任意性。
2二相永磁步進電動機空載磁場有限元計算的不收斂性
二相永磁步進電動機的子具有24個齒(均布),轉(zhuǎn)子具有18個磁極(****磁鋼,N、S均布)。據(jù)其結(jié)構(gòu)特點,可以選擇圓周60o范圍為求解區(qū)域,其余區(qū)域內(nèi)磁場分布與其相同或?qū)ΨQ。圖l是這一區(qū)域的剖分圖,共有344個節(jié)點,630個單元。
利用矢量位A求解,邊界I、Ⅱ具有第一類邊界條件(A—O、,邊界Ⅲ、Ⅳ具有半周期邊界條件  在半周期邊界條件的處理上采用了不降階的處理方法,即在  邊界Ⅲ的節(jié)點上建立方程時,考慮邊界Ⅳ內(nèi)側(cè)單元的作用,而在邊界Ⅳ的節(jié)點上建立方程時,亦考慮邊界Ⅲ內(nèi)側(cè)單元的作用[1]。從而得非線性方程組:
剛度矩陣[K]中的元素是通過A—B
 這一順序過程求得的,K值與A值之間具有較復(fù)雜的關(guān)系。 對式(1)采用傳統(tǒng)的牛頓一拉斐森法(定步長)求解,迭代公式是:
[A]的初值[A](0)的選取是認為規(guī)定媒質(zhì)系數(shù)全部為線性(對于非線性材料,取磁化曲線線性段斜率),將非線性方程組直接作為線性議程組求解一次獲得。
利用這種傳統(tǒng)的方法解算二相永磁步進電動機時,發(fā)現(xiàn)迭代是不收斂的,選擇取了不同的初值,仍得不到收斂結(jié)果,具體表現(xiàn)有兩種,一是迭代進行到某步以后,A值出現(xiàn)振蕩,達不到預(yù)定的精度;二是迭代最初幾步就出現(xiàn)齒磁密大于2.0T的情況,計算無法繼續(xù)。
根據(jù)牛頓一拉非森法的局部收斂性定理,要解決不收斂性,需進一步選擇非常接近
真值的初值[2][A](0)。但是,要選擇這樣的初值,需經(jīng)過反復(fù)的試算,計算量太大,而且,不同的區(qū)域需選擇不同的初值才行,這樣做是很困難的。
通過反復(fù)的摸索,采用了一種稱為可變步長的牛頓一拉非森法,解決了磁場計算中出現(xiàn)的不收斂性,使得初值的選取是大范圍的,提高了收斂性。
3 可變步長的牛頓-拉非森法的實際應(yīng)用
可變步長的牛頓-拉非森法迭代公式為:
與傳統(tǒng)的牛頓一拉非森法(定步長)比較,主要區(qū)別在于增加了變步長因子   變步長因子[ω]<k>可隨迭代步數(shù)的不同而自動調(diào)整。[ω](k)的調(diào)整是依據(jù)于每步迭代的誤差[R]-[F](k)而定的。 在對這臺二相永磁步進電動機空載磁場進行解算時,發(fā)現(xiàn)位于邊界Ⅲ、Ⅳ上的點191,213,...,301;212,234,...3 |






 這一順序過程求得的,K值與A值之間具有較復(fù)雜的關(guān)系。
這一順序過程求得的,K值與A值之間具有較復(fù)雜的關(guān)系。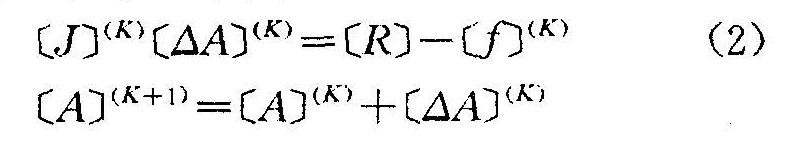
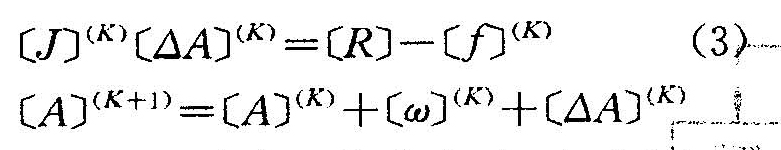

 變步長因子[ω]<k>可隨迭代步數(shù)的不同而自動調(diào)整。[ω](k)的調(diào)整是依據(jù)于每步迭代的誤差[R]-[F](k)而定的。
變步長因子[ω]<k>可隨迭代步數(shù)的不同而自動調(diào)整。[ω](k)的調(diào)整是依據(jù)于每步迭代的誤差[R]-[F](k)而定的。