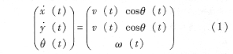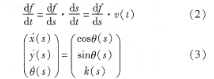一種基于離散化位姿的月球車運動規(guī)劃方法
居鶴華,袁也
(北京工業(yè)大學電子信息與控制工程學院,北京100124)
摘 要:針對障礙環(huán)境下具有非完整約束月球車的運動規(guī)劃問題,提出了一種基于離散化位姿的月球車運動規(guī)劃方法。該方法首先將月球車的運動軌跡限定于多項式旋線,通過求解多項式旋線參數(shù)生成無障礙條件下連接任意位姿狀態(tài)的運動軌跡。同時,該方法對月球車運動規(guī)劃問題中的位姿狀態(tài)空間進行離散化,形成離散化的住姿狀態(tài)空間?根據(jù)離散化位姿狀態(tài)空間的特點,在離線的條件下生成連接相鄰離散位姿的月球車基本的運動軌跡集。最后該方法結(jié)合基本運動軌跡集并利用啟發(fā)式搜索算法最終解決障礙條件下的運動規(guī)劃問題。基于動力學仿真平臺中的實驗結(jié)果驗證了該方法的正確性和有效性。
關(guān)鍵詞:月球車;運動規(guī)劃;參數(shù)化軌跡;離散位姿空間
中圖分類號:tp 273 文獻標識碼:a
1、引 言
月球車運動規(guī)劃系統(tǒng)是月球車導航與控制系統(tǒng)的重要組成部分。其主要目標是在月球環(huán)境下對月球車由起始位姿移動至目標位姿的整個運動過程進行規(guī)劃,使月球車能以安全有效的運動方式移動至目標位。
月球車屬于輪式移動機器人系統(tǒng)的一種,主要的運動規(guī)劃方法包括人工勢場法,ppp方法,快速生成樹方法等。這些方法著重于運動規(guī)劃問題的完整性,使用于實際系統(tǒng)往往存在著困難。jpl研制的火星車所采用的morphin方法則是近年來較為成功的行星車運動規(guī)劃方式。該方法根據(jù)周圍環(huán)境對事先確定的一組運動軌跡進行評價,選擇并執(zhí)行****的運動軌跡。morphin萬法在實際應(yīng)用中取得了很好的效果,但受車載計算能力及機械系統(tǒng)精度的限制,并沒能完全地利用火星車的機動能力。
根據(jù)月球車運動規(guī)劃問題的特點,本文提出了一種基于軌跡參數(shù)求解及位姿空間離散化的月球車運動規(guī)劃方法。
2月球車位姿空間
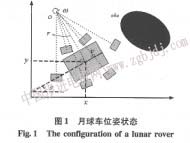
在月球車運動規(guī)劃問題中位姿( configuration)可通過(z,y,θ,k)進行描述。如圖1所示。
(x,y)為月球車在全局坐標系下的位置坐標,日為車體的移動方向,k為車體所在運動軌跡的曲率。其中,曲率^由月球車的驅(qū)動方式及各導向輪的方向角共同決定。在驅(qū)動方式固定的情況下,與各驅(qū)動輪方向角間具有一一對應(yīng)的關(guān)系,可認為是對月球車導向輪姿態(tài)的描述。在月球車的工作區(qū)域中存在著月球車不可穿越的障礙區(qū)域。障礙區(qū)域的具體描述方式由月球車的傳感器系統(tǒng)決定。
月球車運動規(guī)劃目標為,在滿足車體運動約束及避開障礙的同時,使月球車安全且高效的由起始位姿移動至目標位姿。上述運動過程可通過運動軌跡的形式進行描述。
式(1)為月球車的基本運動學約束方程,其中,v(t)為車體平動線速度,w(t)為轉(zhuǎn)動角速度。基本運動學約束為典型的非完整約束,表現(xiàn)為車體不可側(cè)移。一般情況下,月球車在滿足基本運動學約束的同時還受到最小轉(zhuǎn)彎半徑的約束,最小轉(zhuǎn)彎半徑r。。通常由月球車的驅(qū)動方式及各導向輪的擺角范屢決定。
3基于參數(shù)求解的軌跡生成
首先考慮無障礙條件下運動軌跡的生成。車體的基本運動學方程可進行如下變換。令s為表示軌跡弧長的參數(shù),通過式(2)可將式(1)轉(zhuǎn)化為式(3)的形式。其中,k(s) =co(s)/v(s)表示運動軌跡的曲率隨s變化的函數(shù)。式(3)中車體運動方程與時間項分離,可通過函數(shù)k(s),終止弧長s,,及車體沿軌跡移動的速度v(s)描述月球任意的運動軌跡。其中,a(s)及s,決定了運動軌跡在x-y工作空間中的投影,v(s)則決定了月球車沿投影運動的具體方式。兩者相互獨立。
由于確定v(s)需考慮車體在實際移動過程中驅(qū)動控制系統(tǒng)狀態(tài),更適于實時地由驅(qū)動控制系統(tǒng)決定。因此在下文中假定v(s)為常值,將討論的重點放在k(s)及s,的選取。
|