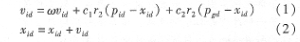摘    要：針對依靠經驗和試驗來確定粒子群優化算法中的參數設定方法存在試驗工作量大且難以得到****的參數組合的問題，提出了一種改進的粒子群算法，該算法利用均勻設計的思想設定算法的****組合參數，把參數設定問題描述為均勻試驗設計中多因素多水平優化設計問題，從而能夠以較少試驗很快設定算法參數的取值，以使算法獲得****性能。仿真試驗表明，利用均勻設計得到的參數組合可使粒子群算法獲得穩健和高效的優化效果，說明了該方法的可行性和有效性，且可以推廣到其他算法參數的設定。

關鍵詞：粒子群算法；均勻設計：參數設定

中圖分類號：tp 18    文獻標識碼：a

    粒子群優化（particle swarm optimization，pso）算法是由kenned j和eherhart r c于1995年提出的一種新型智能計算方法，并在多峰函數優化、多目標優化、神經網絡訓練、控制系統等領域得到充分應用：因此，pso已成為解決復雜優化問題的有效技術，吸引了眾多研究者的關注，新模型、新方法、新應用層出不窮j5。

    雖然粒子群算法發展迅速并取得了可觀的研究成果，但其算法模型中的關鍵參數設置和優化還缺乏成熟的理論指導和研究，目前比較通用的方法是經驗法和試探法。文獻[6]通過大量試驗分析了加速因子對算法收斂性能的影響；文獻[7-8]利用統計方法總結了算法中的種群規模、慣性權值、粒子速度的選擇萬法對算法整體性能的影響效果。但上述研究都足針對具體的研究對象或考察單一參數的沒定，實際上算法中參數之間是相互聯系、相互耦合的，具有復雜的關系，僅僅依靠粗糙的選擇和單參數分析很難找到參數的****組合，而且無法了解參數之間內在聯系。

    為此，本文提出將均勻設計應用于粒子群算法參數設定的方法，將算法中控制參數的設定問題描述成多因素多水平的均勻試驗設計問題，通過較少試驗次數獲得參數的****配置，使算法處于****的運行狀態。

    1)算法原理假設在d維搜索空間中，有m個粒子組成一個粒子群，其中，第i個粒子的空間位置它是優化問題的一個潛在解，將它代人優化目標函數

可計算出相應的適應值，根據適應值可衡量置的優劣；第z個粒子所經歷的****位置稱為其個體歷史****位置，記為pi=(pi1，pi2，pi3，…，pid)；同時，每個粒子還具有各自的飛行速度vi=(vi1,vi2.，…，vid)。所有粒子經歷過的位置中的****位置稱為全局歷史****位置，記pg

=(pg1，pg2，pg3，…，pgd)，相應的適應值為全局歷史****適應值。對每一次迭代，粒子i在d維(1≤d≤d)空間的演化遵循如下方程進行：

式中，m為慣性權值，它使粒子保持運動的慣性，使其有擴展搜索空間的趨勢，從而使算法具有全局搜索的能力；c1和c2都為正常數，稱為加速因子，它使每個粒子向pi和pd位置加速運動，表現出各粒子的自我認知和相互協作r1和r2是2個在[0，1]范圍內變化的隨機數，它可以保證群體的多樣性和搜索的隨機性。

    在優化求解過程中，上述各參數相互聯系，共同維護粒子對全局和局部搜索能力的平衡。

    2)算法流程基本pso算法流程如下：

    step 1初始化設置粒子群的規模、慣性權值、加速因子、****允許迭代次數或適應值誤差限，各粒子的初始位置和初始速度等。

    step 2按目標函數評份各粒子的適應值。

    step 3對每個粒子，比較其當前適應值和其個體歷史****適應值，若當前適應值更優，則令當前適應值為其個體歷史****適應值，并保存當前位置為其個體歷史****位置。

    step 4比較群體所有粒子的當前適應值和全局歷史****適應值，若某粒子的當前適應值更優，則令該粒子的當前適應值為全局歷史****適應值，并保存該粒子的當前位置為全局歷史****位置。

    ste