時滯系統時滯相關型穩定性準則
姜偕富,張忻欣
(杭州電子科技大學自動化學院,浙江杭州310018)
摘 要:針對常數時滯線性系統的穩定性問題,基于一個適當形式的lyapunov-krasovskii泛函,通過利用一個積分不等式,采用時滯分解方法,以線性矩陣不等式的形式給出了時滯系統的時滯相關型穩定性準則。與現有的時滯相關型穩定性結果相比較,所得到的結果具有保守性更好,結構更加簡單,且不含有任何多余的矩陣變量等特點,并從理論上進行了嚴格的證明,解決了現有的穩定性結果絕大多數只是從數值例子說明其有效性的問題。示倒說明了所得結果的有效性。
關鍵詞:時滯;線性矩陣不等式( lmi);lyapunov-krasovskii泛函;穩定性
中圖分類號:tp 27 文獻標識碼:a
1引言
學者們對如何得到具有更小保守性的穩定性結果一直進行著不懈的研究。為了得到具有較小保守性的時滯相關型穩定性結果,近幾年提出了各種不同的方法和改進技術[1-9]。文獻[1]對過去常用的不等式做了改進,得到了一個新的不等式-park不等式,利用該不等式得到的時滯相關型穩定性結果比已有的穩定性結果保守性更小。文獻[3]在文獻[1]提出的park不等式的基礎上做了改進,提出了moon不等式。文獻[4]提出了一種descriptor模型,并以線性矩陣不等式的形式給出了時滯相關型穩定性結果。文獻[5]將文獻[4]中的descriptor模型與文獻[31中的moon不等式相結合,得到了一個更加有效的穩定性結果。文獻[ 6-7]逶過引入自由矩陣變量,不需要對交叉項進行放大處理,避免了由該技術產生的保守性。近一段時間,為了求得保守性小的穩定性準則,人們提出了一種對時滯參數進行分解的方法[8_9],然而文獻[8]中含有多余的矩陣變量,文獻[9]只是從給出的示例說明所得到的結論的有效性,如何尋找一個具有保守性小、結構簡單、所含矩陣變量少的穩定性準則并從理論上嚴格證明其有效性將是本文研究的重點。
2主要結果
考慮如下時滯系統:
式中,x(t)er為系統的狀態向量;φ(t)為初始條件;t>0為系統的常數時滯;a和b為具有適當維數的已知實常數矩陣。
為了給出系統(1)的時滯相關型穩定性準則,首先介紹如下引理。
引理1對于任意的常數矩陣w∈rxn,w= wr >o,標量γ>o,向量函數x:[ -y,0]一r使得下面所涉及的積分有定義,則:
命題1對于給定的常數時滯t,如果存在適當維數的矩陣p>o,
證明 類似于文獻[8],取如下形式的lyapunov-krasovskii泛函:
沿著系統(1)的軌跡對y(z)求導,得到:
那么存在標量a>o時系統(1)是漸近穩定的。對式(4)應用schur補可以得到式(2)。證明完畢。
注1 最近,prof han基于類似的lyapunov-krasovsku泛函:
指出對于給定的時滯參數r >0, 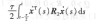 如果存在適應用引理l可得: 那么,有:
|