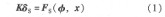靜電諧波微電機(jī)的靜電一結(jié)構(gòu)耦合有限元分析
秦磊1.2,許立忠1
(1 燕山大學(xué),秦皇島066004;2上海微電子裝備有限公司,上海201203)
摘要:該文介紹了靜電諧波微電機(jī)的基本工作原理。通過分析系統(tǒng)中存在的靜電結(jié)構(gòu)耦合關(guān)系,并進(jìn)行離散化處理,建立了結(jié)構(gòu)場和靜電場的有限元耦合平衡方程。討論了靜電場和結(jié)構(gòu)場之間存在的耦合條件和各場的邊界條件。由結(jié)點(diǎn)映射推導(dǎo)出位移和力在兩物理場交界面上傳遞的表達(dá)式。總結(jié)了靜電一結(jié)構(gòu)耦合問題的迭代求解框圖和詳細(xì)步驟。通過對系統(tǒng)的有限元仿真,得到了柔輪的徑向位移分布及其隨系統(tǒng)參數(shù)的變化規(guī)律。所得的結(jié)果為進(jìn)一步研究微電機(jī)的性能提供了依據(jù)。
關(guān)鍵詞:靜電諧波;靜電結(jié)構(gòu)耦合;耦合條件;邊界條件;有限元
中圖分類號:tm359. 9:thl32. 2 文獻(xiàn)標(biāo)志碼:a 文章編號:
0引 言
微機(jī)電系統(tǒng)(mems)是將微細(xì)加工技術(shù)與超精密加工技術(shù)相結(jié)合,以特征尺寸為(0. 5 - 500) ym的可動部件組成的,高度集成機(jī)械、電子與控制于一體的系統(tǒng)。隨著系統(tǒng)尺寸的不斷減小,靜電力表現(xiàn)出比機(jī)械力和電磁力更明顯的優(yōu)勢。靜電驅(qū)動逐漸成為mems領(lǐng)域最常用的驅(qū)動方式。研究多能量域耦合問題則一直是mems領(lǐng)域關(guān)注的重要課題。
endemano等給出了一種醫(yī)用雙定子雙轉(zhuǎn)子的擺動式靜電電機(jī)的扭矩計算模型;saitos t等闡述了具有8個定子電極的圓柱式和圓錐式擺動靜電電機(jī)的設(shè)計結(jié)構(gòu),并進(jìn)行了一系列分析和測試。他們提出的模型均存在輸出軸擺動,轉(zhuǎn)子與定子之間由于摩擦導(dǎo)致靜電能損失等缺陷。本文基于諧波傳動原理提出一種新型靜電驅(qū)動電機(jī)——靜電諧波微電機(jī)。
1靜電諧波微電機(jī)的工作原理
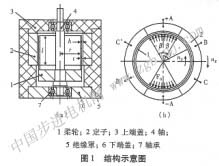
如圖l所示為靜電諧波微電機(jī)的結(jié)構(gòu)示意圖。圖l(a)中,傳動的柔輪1是半徑為r、壁犀為h,有效變形長度為l的薄壁鋁制圓柱,柔輪外面是厚度為t的薄層空氣。定子是空氣層之外的6塊用來在不同時刻施加電壓的互相絕緣的金屬導(dǎo)體2,它們的內(nèi)壁需經(jīng)過陽極氧化處理,以獲得一層很薄的電靜電諧波微電機(jī)的靜電一結(jié)構(gòu)耦合有限元分析秦磊,等介質(zhì)層。如圖l(b)所示,在定子2的兩個相對的對稱角度[ -p,p]即扇區(qū)aa上施加幅值相等、極性
相反的電壓后,會在柔輪1的表面產(chǎn)生一定的感應(yīng)電荷,于是內(nèi)外金屬體之間形成靜電場,所產(chǎn)生的電場力如圖中所示。在靜電場力的作用下,柔輪必然會發(fā)生一定的變形。將幅值相等、極性相反的電壓按/所示方向順序施加于不同的相對應(yīng)的兩個扇區(qū)aa,bb和cc內(nèi)則柔輪會在相應(yīng)的位置發(fā)生變形,由于變形的周期性,柔輪會因此而沿n。所示方向轉(zhuǎn)動起來。如上所述,a,b,c,a,b和c為6路幅值相等的直流開關(guān)信號,同一時刻僅兩個對應(yīng)扇區(qū)施加極性相反的電壓,并將這種電壓施加方式沿某一方向順序切換至下一扇區(qū)。
在靜電諧波微電機(jī)系統(tǒng)中,靜電驅(qū)動使柔輪發(fā)生變形從而產(chǎn)生運(yùn)動,變形的柔輪又反過來改變了靜電場的分布,如此反復(fù)直至平衡。系統(tǒng)的正常運(yùn)轉(zhuǎn)有賴于柔輪的變形,準(zhǔn)確而高效地分析柔輪在靜電場力作用下的變形是研究系統(tǒng)承載能力的關(guān)鍵所在。本文基于對系統(tǒng)耦合關(guān)系的分析,建立了有限元耦合平衡方程,探討其耦合條件和邊界條件,并重點(diǎn)給出了柔輪徑向位移的分布規(guī)律。
2靜電一結(jié)構(gòu)耦合方程
2.1結(jié)構(gòu)場平衡方程
當(dāng)電壓緩慢地施加于靜電場的邊界上時,整個耦合問題可視為是靜態(tài)的。靜電諧波微電機(jī)的柔輪受外層電場的作用將發(fā)生變形,遵循彈性結(jié)構(gòu)有限元理論的力平衡方程:
其中,k為結(jié)構(gòu)場的整體剛度矩陣;δs為結(jié)點(diǎn)位移列陣;fs(φ,x)為電場作用于柔輪的力向量,很顯然,電場力的大小由靜電場的電勢西和電場內(nèi)結(jié)點(diǎn)的位移x共同決定。
2.2靜電場平衡方程
柔輪外層的電場可由拉普拉斯方程及其邊界條件來描述:
|