改進的遞推主元分析及遞推主元回歸算法

  程龍，王桂增

(清華大學自動化系，北京100084)

   摘    要：為了加速模型在線更新的速度以更好地適應實際工業過程的動態變化，通過在已有遞推主元分析(PCA)算法的基礎上簡化了自相關矩陣的遞推公式，從而改進了基于秩1更新的遞推PCA算法，把原來需要進行2次秩1更新的步驟簡化為僅僅需要進行一次秩1更新，并在此基礎上提出了遞推主元回歸算法。仿真結果表明，改進后的基于秩1更新的遞推PCA算法比原來的基于秩l曼新的遞推PCA算法縮短了近一半的運算時間，而新的遞推主元回歸算法，不但能夠適應工業過程的動態變化，并且比批處理的方式節約了存儲空間與計算時間。

關鍵詞：遞推主元分析；自相關陣；秩1更新；遞稚主元回歸

中圖分類號：TP 27    文獻標識碼：A

Improved Recursive PCA a nd Recursive PCR Algorithms

    CHENG Long，WANG Gui-zeng

    (Department ofAutomation．Tsinghua University，Beringl00084，China)

Abstract．To accelerate the model 0n-line modificatlon a nd accommodate the industrial process change，an efficient recursive PCA al-gorithm using rank-one modification a nd a novel recursive PCR algorithm are proposed by improving the approach of updating correlationmatrix  Simulation resuits show that the improved recursive PCA based on rank-one modification shotren the computational time in con-trast with the existing recursive PCA algorithm  Moreover．the recursive PCR algorithm Call adapt process changes a nd need less corn-puting time a nd memm?usage than batch PCR algorithm

Key words：reellisive PCA；coneiation matrix；rank-one modification；recursive PCR

1引言

主元分析(PCA)是一種將多個相關變量轉化為少數幾個相互獨立變量的統計分析方法。

  主元分析由Pearson^[1]最早提出，后經Hoteling^[2]加以改進。主元分析可以將很多相關過程變量壓縮為少數獨立的變量，因此被廣泛應用于過程監控^[3]，故障診斷^[4]等領域。

    實際的工業過程通常表現出時變特性，用主元分析法建立的模型隨著時間的推移將出現明顯的偏差，為此，需及時對模型進行更新，而如果采用將新數據和舊數據結合重新進行主元分析，計算量很大。針對上述情況，Wold提出了指數加權平均主元分析的方法^[5]，Rigopoulos等提出了滑動窗結合主元分析的方法^[6]，而Liw H等提出了遞推PCA算法^[7]，對數據矩陣的均值、標準差進行遞推更新，從而遞推求出規范化后的數據矩陣，進而得出自相關陣的更新公式，最后利用秩1更新得出負荷向量和得分向量。

     本文針對Li WH等提出的遞推PCA算法，簡化了自相關陣的遞推公式，改進了基于秩1更新的遞推PCA算法，并給出了輸入輸出變量協方差矩陣的遞推公式，提出了一種新的主元回歸遞推算法(PCR)，仿真實驗證明了方法的有效性。

2改進的遞推PCA遞推算法

  1)基于秩1更薪的遞推PCA算法定義全部k個原始輸入數據塊組成的矩陣為

    其中，每一行代表一個樣本，每一列代表一個輸入變量。

    全部(k+1)個原始數據塊組成的矩陣為X^o_k+1形式與X^o_k相同。若前K個數據塊長度為Mk，考慮每采樣一次進行一次遞推，則包括新來數據的所有(k+1)個數據塊的長度為N_k+1=N_k+1。Weihua Li H指出^[7]，每當新數據x⁰_k+1來時。可以遞推計算出原始輸入數據矩陣中各變量的均值、標準差和規范化后的輸人數據矩陣，進而得出自相關陣的遞推公式。

  均值向量的遞推式為

    上述各遞推式中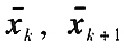，分別是遞推前后均值向量，且為行向量，每一元素為對應輸入變量的均值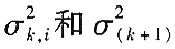；i分別為遞推前后第i個變量的方差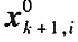，為新來數據向量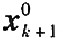的第i個元素；R和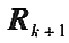分別為遞推前后規范化后輸人數據陣的自相關矩陣；考慮規范化后的新來數據向量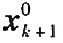后的輸入自變量的均值向量的增量為圖---

式中,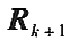為對角陣,對角線元素為di(i=1,2,...,m),ε為常數.

    可以證明^[8],下面m次有理多項式的m個根對應于更新過的自相關矩陣的m個特征值λⁱ。

特征值λⁱ所對應的單位特征向量Pⁱ可以通過下列計算：

    Wemua Li H進一步指出。^[7]可以用上述秩1更新的方法，利用R^k已經得出的特征值及特征向量信息結合自相關陣的遞推公式得出更新過的負荷向量與得分向量。

    設前一次自相關矩陣特征分解的結果為R_k=P_kA_kP_TK，其中，P_K每一列為單位特征向量，A_K是對角矩陣，對角線上的元素為特征值。由于R_K為對稱矩陣，所以P_K是正交矩陣。

    把前一次自相關矩陣特征分解的結果代人自相關矩陣的遞推計算式中得到：

式中，A_k2為對角矩陣，對角線上的元素為修正過的特征值；P_k+1=P_KP_K1P_K2，其單位化后的每一列即為更新過的協方差矩陣R_K+1的特征向量(負荷向量)。

    2)改進的秩1更新遞推P_cA算法由于：

式中,P_k+1=P_kP_k+1,其每一列為更新過的相關矩陣P_k+1的單位特征向量(負荷向量)。

    與原來的秩l更新遞推PCA算法相比，改進過的算法只需要進行一次秩1更新就可以求出負荷向量，大大縮短了計算時間，且精度不變。

3主元回歸PCR的遞推算法

    1)輸入輸出變量協方差陣的遞推計算  在PCR中，需要對輸出數據陣也進行規范化處理。其中輸出數據陣的形式如下：

同樣考慮每來一個新數據就遞推一次的情況，仿照輸入數據矩陣各參數遞推式的推導，可得輸出變量的均值向量的遞推式為

式中,為規范化后的新來數據.仿照自相關矩陣的簡化遞推公式的推導,協方差矩陣進一步可簡化:

    2)算法流程主元回歸(PCR)首先在自變量

空間進行主成分分析(PCA)，即將高維相關的原始變量投影到低維正交的特征變量空間上，再建立特征變量同輸出間的回歸關系。

    設輸入輸出關系為

式中，a為取前α個主元；β為主元回歸模型的的回歸系數向量。

    因此不用重新計算規范化后的輸入輸出變量的數據矩陣，而僅僅遞推計算自變量的自相關陣和自變量因變量的協方差陣就能更新PCR的回歸系數。

    注意，這里的b^{^}_PCR是將主元回歸模型轉換為以原始變量作為輸入變量時所得到的偏最小二乘回歸模型的系數向量，而不是一般意義上的以原始變量作為輸入變量時的最小二乘回歸模型的系數向量。

    遞推PCR的算法流程如下：

    ①每來一組新數據，遞推計算輸人輸出變量數據矩陣的均值，標準差，進而計算自相關陣R和協方差陣R_xy。

    ②由R的遞推式采用秩1更新遞推計算負荷向量。

    ③取前α個負荷向量組成負荷向量陣Pα，Pα的每一列對應一個負荷向量，把R，R，Pα代人式(28)中，更新PCR模型。

    ④對此后到來的新樣本(輸人數據)，采用新的PCR模型對輸出進行預報。

    在上述遞推PCR算法中，僅需要存儲前一次遞推計算的均值向量、標準差、自相關陣、協方差陣，不用存儲原始輸入輸出數據陣，而均值向量、標準差、自相關陣、協方差陣的維數只與變量個數有關，因此大大減少了存儲空間。隨著數據的不斷增加，如果采用批處理，存儲空間將不斷增大，而采用遞推算法，存儲空間沒有變化。

4 PCR仿真結果與分析

    下面以聚酯生產中終縮聚特性黏度的軟測量建模為例，利用遞推PCA算法提取得分向量與負荷向量，再建立起對應的主元回歸模型(PCR)，對聚酯特性黏度值進行估計。

    特性黏度是聚酯切片最重要的質量指標，是表征分子量的參數。由于聚合物分子量與其物理機械性能有密切關系，加工后要求分子量控制在一定范圍內，且生產中要求分子量基本不變化。而特性黏度是無法直接測量的參數，且與諸多因素有關，如最終縮聚釜和離開最終縮聚釜的熔體特性黏度、反應溫度、反應壓力、攪拌器轉速、反應物料在釜內的停留時間、催化劑濃度等。

    1)數據選擇選取在連續時間段實際測量的700組數據進行仿真實驗。其中，選取10個與特性黏度相關的變量作為輸入，而特性黏度的分析值作為輸出。

    把700組數據分為3組，前300組數據作為初始建模數據，中間300組數據作為更新數據，最后100組數據作為測試數據。

  特性黏度分析值趨勢圖，如圖1所示。

   由圖可見，前300組數據，特性黏度分析值變化比較大(而實際輸入自變量變化比較緩慢)，從第300組開始，特性黏度分析值變化較為緩慢。從理論上，僅僅用前300組數據建立起的模型預測最后100組分析值是不夠準確的，必須采用遞推算法更新模型。

  2)遞推算法的運行時間比較在遞推算法中，首先提取前300組數據的主元建立PCR模型，然后按照前面提到的遞推PCR方法流程，用中間300組數據進行PCR模型的遞推計算所得到的更新模型對后。100組數據進行輸出估計，并與取前600組數據用PCR批處理方法所得的模型進行輸出估計的時間進行比較，結果見表1。

   由表1可知，利用遞推公式更新參數較之批處理方法重新在整個數據集上計算模型參數的計算時間縮短近2／3。

    求解負荷向量的計算時間，見表2。

   由表2可以看出，改進過的基于秩l更新的遞推PCA算法與原來的基于秩1更新的遞推PCA算法相比減少一次秩l修正的步驟，計算時間縮短了約一半。

  3)遞推PCR算法的結果精度比較遞推PCR算法相對于傳統PCR算法的一個重要優點就是可以實時更新模型參數，從而使模型更好地適應工況的變化，使估計結果更準確。 

2種模型對測試集(100組數據)進行估計的模型殘差平方和的比較，見表3。

    表3中的非遞推PCR算法僅用前300組數據進行建模，而改進后基于秩l更新的遞推算法在前300組數據模型的基礎上用中間的：300組數據進行遞推計算，而這300組數據在實際測量時相當于新來數據，也就是說，對原來在300組數據基礎上建立起來的模型進行了更新，其實在實際生產中，只要來了一組新數據，就可以馬上對模型施行更新，進而用更新過的模型進行預測。

    由表3可以知，遞推算法所得模型的估計性能優于非遞推算法時的模型性能。

5結語

    本文在已有的遞推PCA算法的基礎上，簡化了自相關陣的更薪公式，改進了基于秩1更新的遞推PCA算法，并提出了一種新的遞推PCR算法。

    仿真實驗表明，遞推算法所建建模比不采用遞推算法所得模型跟蹤效果要好。改進后的基于秩l更新的遞推PCA算法不但在保持了原基于秩1更新的遞推算法的精度，而且縮短了計算時間。在此基礎上得到的遞推主元分析算法，不僅能夠適應過程的動態變化，且比批處理的方式節約了存儲空間與計算時間。