摘  要：由于行波超聲波電機存在時變性、非線性等特征，為了得到更加穩定的轉速輸出，利用神經元的自學習能力在線尋找****控制參數，是提高電機控制效果的有效途徑。因此通過分析單神經元PID控制器優缺點，可以利用單神經元PID和PI構成復合控制器，提高行波超聲波電機的速度控制效果，而且結構簡單，有利于商品化。
　　關鍵詞：超聲波電機；單神經元PID；復合控制；實驗

     0  引  言智能化、數字化的機電一體化技術成為當今世界工業科技領域發展的焦點和熱點之一。近年來，超聲波電機作為一種直接驅動電機取得了飛速發展，并且在伺服控制方面日益表現出優良的工作特性。超聲波電機的推廣應用只有結合有效的控制方法和控制策略，才能充分發揮其****性能。由于受到超聲波電機運行機理的影響，電機輸入輸出之間存在明顯的非線性關系_。因此本文在分析單神經元PID控制特點的基礎上，利用單神經元PID的自學習自適應功能，通過單神經元PID—PI復合控制器實現了對行波超聲波電機變參數控制，這種控制器既具有一定的克服電機非線性能力，其結構又相對比較簡單，更利于實用化應用.
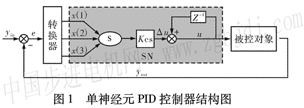
　　1  單神經元PID的特點神經網絡的基本組成部分為單神經元，而單神經元PID是一種比較實用的具有自學習功能的PID控制器。控制器的結構如圖1所示。圖中yin(k)、yout(k)分別為控制器的輸入設定值和輸出。
　　圖中的灰色部分為單神經元PID調節器，調節器的輸入x1(k)、x2(k)、x3(k)分別為神經元積分項、比例項、微分項系數學習所需要的誤差函數。

　　由于其為增量式結構，所以有：

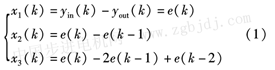
　　神經元是通過權值系數的調整來實現自學習功能的。其控制算法為

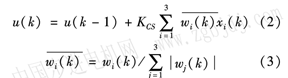
　　式中，ωi(k)=(i=1，2，3)分別為積分項、比例項、微分項的權值；Kcs為單神經元PID的控制參數增益。
　　通常單神經元PID自學習采用有監督的Hebb學習算法。單神經元PID權值調整的具體學習算法為：

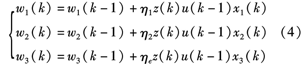
　　式中，ηi(i=1，2，3)分別為積分項、比例項、微分項的學習速率；z(k)為誤差信號。
　　在式(4)中，z(k)作為為教師信號，電機的輸入和調節器的輸入x1(k)、x2(k)、x3(k)分別為積分項、比例項、微分項權值的激勵輸入。神經元將根據激勵輸入，使積分項、比例項、微分項的權值向誤差減小的方向調整。因此當電機在轉速調節過程中遇到的非線性和時變性，可以利用神經元的自學習特點來克服。但由于學習算法的結構特點，其權值特別是積分項權值ω1(k)的變化過程與誤差的平方有關，當誤差長時間出現過大時，該項參數會變得過大，會影響到學習效果，甚至發生溢出現象。
　　2  單神經元PID—PI復合控制器設計

     為了避免神經元PID在長時間大誤差情況下出現的溢出情況，本節將設計由常規PI和單神經元PID構成的復合控制器。在大誤差情況下利用常規PI進行調節，而在誤差較小的情況下則利用單神經元PID的自學習能力使電機轉速能達到比較理想的運行效果，并減輕由電機時變性引起的常規PI參數整定的困難。
　　圖2為該控制器的結構圖。速度控制的反饋信號來自于反映電機位置變化的光電編碼器位置信號θout控制器利用該位置信號，通過T測速法，計算出電機當前轉速nout作為其反饋量。圖中nin為設置轉速。

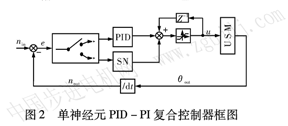
　　控制器根據輸入設定轉速與實際轉速差e來確定采用何種控制算法，當電機的誤差大于設定誤差時，電機將以常規PI方式運行，當實際轉速接近設定轉速時，控制器則采用單神經元PID算法，對電機轉速進行精確控制。本文中為了避免算法在誤差切換點的頻繁切換，算法中還需設置誤差環寬，即當誤差的****值小于1 5 r／min時采用單神經元PID控制，當誤差大于25 r／min時采用常規PI控制，若誤差在環寬內則算法保持不變。PI控制算式采用增量式：
　　△u(k)=kp△e(k)+K i e(k)    (5)

      式中，△e(k)=e(k)一e(k一1)；K p為比例增益；K1為積分增益。在控制中，控制器的實際輸出量為u(k)=u(k一1)+△uo

3  單神經元PID—PI轉速控制實現

        利用上節設計的單神經元PID—PI復合控制器，本節將對其在恒轉速控制、轉速跟蹤控制的控制效果進行驗證，并與常規PID控制效果進行比對。實驗電機為本課題組研制的直徑60 mm的行波超聲波電機TUSM60。其控制系統如圖3所示。

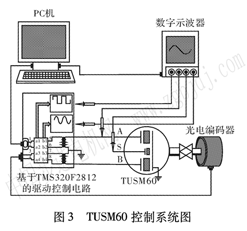
　　該控制系統中采用TMS320F28 1 2作為控制核心，驅動采用全橋方式。DSP與PC機相連，接受轉速設置信號。在驅動控制電路中設有D／A輸出接口和數字輸出接口，以便將控制算法的中間結果和電機實際運行狀態實時送至示波器并記錄以便分析。電機狀態傳感器采用1 0000線光電編碼器。DSP芯片利用T法通過捕捉光電編碼器脈沖邊沿來計算轉速，并利用控制算法，通過PWM波的頻率，即電機驅動頻率來調節電機轉速。
　　當改變驅動頻率作為調節手段時，由于行波超聲波電機工作在諧振點的右側，所以頻率減小振幅才能升高，因此可規定：
　　fd(k)=fs—lu(k)l    (6)式中，．fd為實際驅動頻率；．fs為頻率的調節上限。
　　文中所用電機的上限頻率為44．75 kHz。u(k)的正負號由兩相驅動的相位差來表示，當u(k)≥O時，φ=π／2，當u(k)　　3．1  轉速控制階躍響應

      當設定轉速為120 r／min時采用常規PI控制時的轉速階躍響應曲線見圖4。

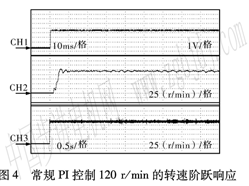
　　圖中CHl為標識電平。該信號的跳變代表階躍開始，即O時刻。CH2為實際轉速變化過程。
　　它們的時間刻度為10 ms每格。CH3為行波超聲波電機轉速穩態情況，時間刻度為O．5 s每格。在起動階段，轉速響應過程的上升時間為4 ms左右，超調量為9％左右，調整時間為8 ms。由于行波超聲波電機具有時變特性，從較長時間反映轉速穩定性的CH3轉速曲線可以看出，電機在運行一段時間后，轉速出現抖動，抖動誤差為±1 O％，電機運行并不穩定。

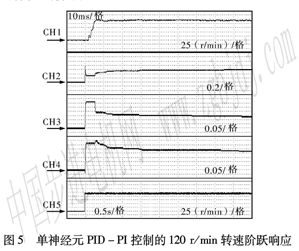
　　單神經元PID—PI復合控制效果如圖5所示。
　　圖中CHl～CH4分別為轉速以及權值系數ω1(k)～ω3(k)的變化過程，時間刻度為1 O ms每格。CH5為電機穩態時的運行情況，時間刻度為O．5 s每格。
　　由于權值設有初值，所以在電機階躍信號給定的瞬間權值系數會有跳變，但此時由于誤差大于15 r／min權值系數跳變后維持不變，單神經元PID并不起作用。權值系數跳變可以看作階躍給定，即O時刻的開始。當電機轉速升至105 r／min后，控制器進入單神經元PID控制狀態，權值系數開始發生改變。在整個起動過程中，超調量為4．5％，上升時間為3．5 ms，調整時間9 ms。在單神經元PID—PI復合控制下，上升時間和調整時間與常規PI控制相近，超調略小，兩者指標接近，單神經元PID—PI復合控制并無明顯優勢。由于受到電機時變等特性的影響，電機在進入穩態后權值仍然會有所調整，以適應電機特性的變化。從CH5電機穩態時的運行效果可以看出，由于單神經PID的自學習自適應能力使控制參數隨電機特性時變而調整使轉速保持穩定，此時利用單神經PID克服電機時變性的特點得以發揮。
　　3．2轉速跟蹤控制

     圖6為使用常規PI控制器對TuSM60進行轉速正弦軌跡跟蹤控制結果。其中CHl為電機實際轉速，CH2為被跟蹤軌跡。該軌跡為頻率O．5 Hz幅值60 r／min的正弦曲線。CH3為跟蹤誤差，****跟蹤誤差出現在轉速為O附近，約11 r／min左右。

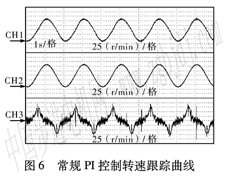
　　由于行波超聲波電機具有明顯的非線性，固定參數的PI控制無法同時滿足在各個運行范圍內都具有比較好的控制效果，在此控制下部分轉速點的誤差會有較大的抖動尖刺，運行并不穩定。
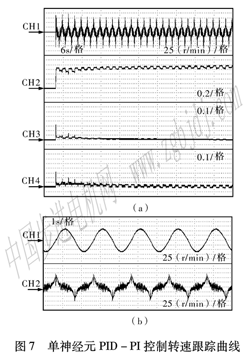
　　由于單神經元PID具有在線自學習能力和自適應能力，因此在轉速跟蹤控制中，可利用單神經元的這種變參數控制特性，解決因電機非線性對控制參數整定帶來的難題。圖7為與圖6具有相同的設置頻率和轉速幅值時，單神經元PID—PI復合控制的正弦軌跡跟蹤控制效果。由于大部分情況下，跟蹤誤差都可以控制在切換誤差的環寬以內，　　所以跟蹤誤差很大程度上依賴于單神經元PID控制器的控制能力。圖(a)為跟蹤控制過程中跟蹤誤差以及權值系數的學習變化過程。其中CHI．為跟蹤誤差，CH2～CH4為權值系數ω1(k)～ω3(k)，時間刻度為6 s每格。圖(b)的CHI．、CH2為實際轉速變化過程以及與之對應的跟蹤誤差，時間刻度為：1 s每格。從圖(a)的CHl中可以看出，在電機運行的初始階段，跟蹤波型的單周期內****誤差為：1 1 r／min，并且與常規PID控制相似，電機轉速在個別點并不穩定。但隨神經元權值的調整，電機轉速在單周期內的****誤差逐漸減小，8個周期后減至7．5 r／min。與常規PID控制的結果相比較，在單神經元PID控制下轉速跟蹤的****誤差降低了1 7％，同時電機的轉速穩定性也有所提高。

　　4  結  語

     通過單神經元PID的自學習能力，在線調節控制器參數，以適應行波超聲波電機非線性和時變性，特別是在轉速跟蹤控制中，可以綜合平衡****跟蹤誤差和轉速穩定性之間的矛盾，這是固定參數的常規PID控制難以做到的。同時單神經元PID控制的參數整定通常只需要調整參數增益kcs在實際控制過程中可以減少控制效果對人為因素的依賴。