胡笳,趙海森,劉明基,羅應立。
(1 中國電力國際有限公司,北京100080;2華北電力大學電氣與電子工程學院,北京102206)
摘要:永磁l司步電機運行時鐵心損耗分布不均勻,在利用時步有限元進行計算時,空間離散密度的選取將對其計算精度造成影響。因此,首先利用時步有限兀方法求得電機鐵心中損耗的分布曲面,在此基礎上通過插值計算的方法對該曲面不同離散情況下的誤差進行預測分析,得出損耗誤差隨離散密度的變化規律,并針對轉子渦流損耗計算中高次諧波所產生的混疊現象,對時間步長的選取進行r相關討論;最后通過對比一臺55 kw永磁同步電機的仿真與實測結果,驗證了該方法的合理眭。
關鍵詞:時步有限元;永磁電機;鐵心損耗;空間離散;時問離散
中圖分類號:TM 351 文獻標志碼:A文章編號:1673 6540(201O)09-0001_07
O 引 言
永磁同步電動機(Perenent Mgnet synch nJ-nous Molr,PMsM)以其高效率、高功率因數等特點,已成為高效節能電機的重要發展方向之一:
其中鐵心損耗作為電機總損耗中的一部分,對電機的效率及運行性能有著直接的影響,從而在利用時步有限元對永磁電機進行設計研究時,如何對其進行準確計算具有重要的實際意義:
PMsM正常運行時,交變的磁場將在定、轉子鐵心中作用產生渦流與磁滯損耗:傳統的鐵耗計算公式{1-4}是在磁場正弦規律變化的基礎上得出的。對于實際運行的永磁電機,其中磁場往往包含多種諧波成分。文獻[5—8]提出了考慮諧波情況下利用時步有限元計算鐵心渦流損耗的方法,該方法通過磁密的變化率可計算含有不同次數諧波成分作用下鐵心的平均渦流損耗。另外對于鐵心中的旋轉磁化部分,可將其磁密分別沿徑向、叨向正交分解后進行計算{9-11}。
在利用時步有限元方法計算鐵心損耗時,由于鐵心中的損耗分布不均勻,從而空間的離散密 度將對損耗計算結果的精度造成直接影響。另外,考慮到轉子鐵心中主要含有高次諧波磁場,時間步長的選取若仍按照傳統計算起動性能的情況進行考慮,將可能由于發生混疊現象{12-15}導致產生計算誤差甚至出現嚴重錯誤。針對以上問題,本文系統地分析了時步有限元計算中時問與空間離散密度對鐵心損耗計算精度的影響。通過與現場實測結果進行對比,說明了該方法的合理性。
1永磁電機鐵耗計算
1.1解析計算方法


1.2時步有限元計算方法
在利用時步有限元方法計算永磁電機鐵心損耗時,首先可通過求解電磁場方程,得出電機不同工況下穩態運行時的節點磁位,進而根據相應位置的磁密結果計算其損耗密度及損耗。本文以某廠55 kW的PMSM為例,采用二維平面場進行計算,求解區域如圖1所示,通過麥克斯韋方程組得到求解區域的電磁場基本方程:
 

2 空間離散
根據上文分析,研究空間離散密度對鐵心損耗計算的影響(以渦流損耗為例),首先需要確定計算區域的損耗分布曲而ped(x,y)。對于實際運行的永磁電機,空間磁場由定子電流、永磁體及轉子導條中的感應電流共同作用產生;同時考慮鐵磁材料的非線性等因素,鐵心中損耗分布的規律f‘分復雜,且隨著運行工況的不同發生改變,難以得到其準確的解析表達式。為此本文采用以下方法進行處理。
(1)分別選擇電機定、轉子鐵心中某齒部及軛部作為研究區域,對其進行細化的剖分離散(滿足當采用更細化的剖分時,損耗的計算結果差別不大);

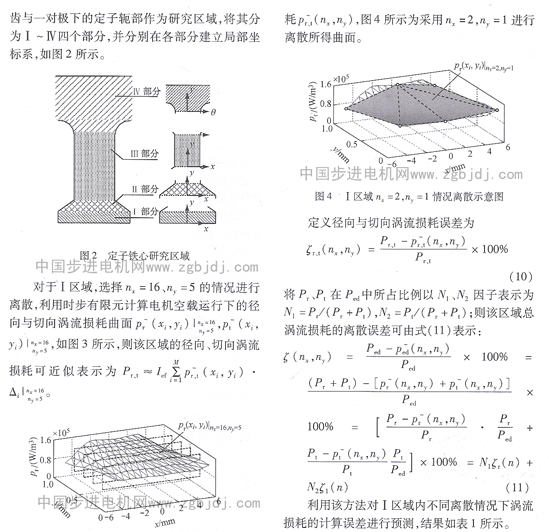
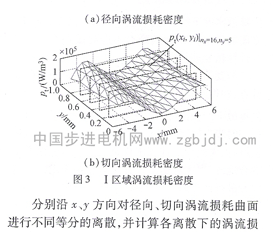 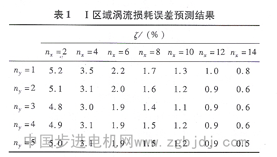
可見,對于定子齒頂區域,沿圖周方向的離散份數對損耗計算的誤差影響較大。為了驗證該方法所得預測結果的合理性,針對I區域不同的剖分情況,直接利用時步有限元方法計算其損耗誤差,結果如表2所示。
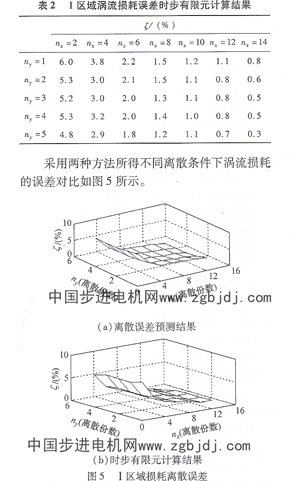
可見,兩種方法所得誤差分析結果基本相同,從而說明了誤差預測的合理性,進而可根據該誤差預測的結果,確定渦流損耗計算時定子鐵心各部分區域的空間離散策略。
對于定子鐵心Ⅱ~Ⅳ區域,同樣參照上述方法進行不同離散下的渦流損耗預測計算,圖6為Ⅱ區域切向渦流損耗與Ⅲ區域徑向渦流損耗曲面(其他結果圖略),圖7為Ⅱ、Ⅳ區域損耗隨離散密度的誤差曲面(對于Ⅲ區域,由于其p,(x,y)、p,(x,y)近似均勻分布,從而認為該區域滑x、y方向的離散密度對渦流損耗的計算基本無影響)。
2.2轉子鐵心
對于PMsM,轉子鐵心中的渦流損耗主要由
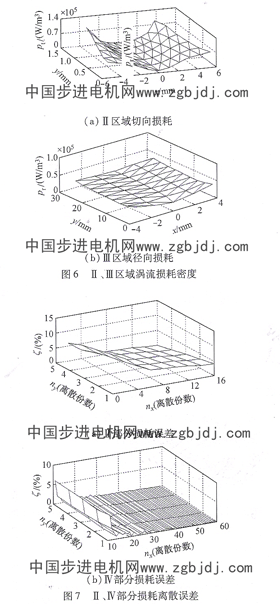
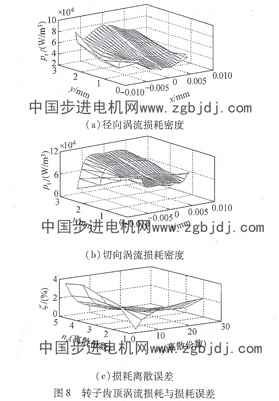
諧波磁場產生,且主要集中于轉子齒頂部位。通過有限元計算,本文所分析的55 kw永磁電機穩態運行時,齒頂處的渦流損耗可占整個轉子渦流損耗的83%~85%,從而關于轉子鐵心離散策略的研究即主要歸結為轉子齒頂離散密度對渦流損耗計算精度影響的研究。
參照定子鐵心的處理方法對轉子齒頂區域進行計算,相應的損耗曲面如圖8所示
對于不同離散條件下電機磁滯損耗的誤差預測同樣可采用上述方法進行分析計算。
3 時間離散
在利用時步有限元方法分析PMsM鐵心損耗時,除了空間離散外時間的離散也將對損耗的計算精度產生影響,尤其是對于轉子鐵心渦流損耗的計算。由于該損耗主要由諧波磁場產生,在利用dB/出=(B{j+1} B{j})/t進行計算處理時,若△t的選取不恰當,將使得渦流損耗的計算結果產生極大的誤差,甚至導致結果嚴重錯誤。
因為一般在利用時步有限元計算電機起動性能的分析中,往往主要關心的是類似定子電流等電氣量的基波含量(或其低次諧波),此時對于時間步長的選擇△t=T1/50(其中T1為基波的周期),即在一個基波范圍內離散50份就可滿足計算精度要求。但是,在計算PMsM轉子鐵心渦流損耗時,由于其主要由諧波磁場產生,特別是當含有類似齒諧波這樣的高次諧波所產生的損耗時,若仍

4試驗對比
對55 kw永磁電機樣機進行現場實測,并根據本文提出的時空離散策略對其進行時步有限元計算。對比不同負載情況F的測試與計算結果,如表3所示。

Ptc,Ptm分別為電機鐵耗的計算值與實測值,其中鐵耗實測值通過電機的總損耗減去定、轉子銅耗得到,由于轉子銅耗難以實測得出,從而采用有限元計算結果。考慮機械損耗與附加損耗時,仿真計算與現場實測所得結果在誤差范圍之內。
5 結 語
在利用時步有限元計算PMsM鐵心損耗時,為了得到準確的計算結果,本文針對定、轉子鐵心空問離散及時步計算過程中所涉及的時間離散問題上進行了相關研究。提出了不同離散情況F鐵心損耗的誤差預測方法,為得到相應的空問離散策略提供依據。對于時間離散的問題,研究表明:
采用時步有限元計算永磁電機鐵心損耗時(尤其是轉子渦流損耗),需根據采樣定理保證所計及****次數諧波(一般為齒諧波)不發生混疊現象為依據來選擇時間步長。
|